Maxwell velocity distribution (이상기체 탄성 충돌 시뮬레이션)

시뮬레이션 목적

  1. 경우의수로 기술되는 통계물리와 충돌을 통해 에너지를 교환하는 실제 세상과 비교

   1) 평형 상태에서 입자들이 위치적으로 균등하게 있는지 확인

   2) 평형 상태에서 맥스웰-볼츠만 속도 분포 확인

   3) 에너지를 교환할 때 ΔE 의 분포가 볼츠만 분포를 따르는지 확인

   4) 낮은 에너지(속도)의 입자는 에너지의 변화의 기대값이 0보다 크고

     높은 에너지(속도)의 입자는 에너지의 변화의 기대값이 0보다 작음을 확인 

시뮬레이션 조건

1. 차원 : 2차원   2. 면적 L*L : 3000*3000   2. 입자의 개수 N : 10000개   3. 입자 지름 R : 3   4. 입자 무게 m : 1   5. 볼츠만 상수 kb : 1   * 단위 생략

시뮬레이션 방법

  1. 입자 N개의 초기조건  (다른 속력 분포로 시뮬레이션 2번 실시)

   1) 위치 분포 :   0<x<L     0<y<L  사이 균등 난수 부여

   2) 속력 분포 :  -1<v_x<1   -1<v_y<1  //  -2<v_x<2   -2<v_y<2  사이 균등 난수 부여

  2. 단위시간 Δt : 0.005 로 잡아서 입자의 위치를 업데이트 한다.

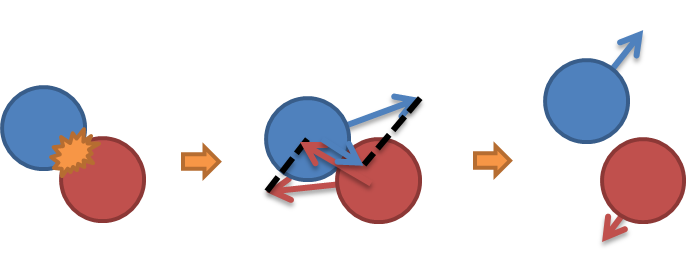
  3. 업데이트 후 입자간의 거리가 R보다 작아지면 충돌했다고 판정하고 탄성충돌을 통해 속도 변환

   ( 충돌면에서 수직한 속도 성분을 교환시킴  (그림 참고) ) 

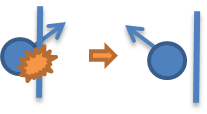
  4. 경계면( x=0 or x=L or y=0 or y=L ) 을 넘어가면 되튀게 함

  5. 평형을 이룰 때까지 반복

시뮬레이션 결과

   탄성충돌만 일어나므로 입자의 갯수와 에너지가 고정된 시스템 (isolated system) 이지만 canonical distribution에서

   입자가 많아지면 에너지 평균치가 한 값으로 대체할수 있으므로 canonical distribtution으로 근사 가능하다.

   즉 초기 조건에 따라서 에너지가 고정되는데 이것이 온도 T가 주어진 것으로 생각해도 좋다.

   T = <v²/2> ( 등분배 정리, 2차원 )

   초기 조건을 다르게 하여 온도를 다르게 시뮬레이션 2번 실시 :   

   -1<v_x<1  -1<v_y<1  인 경우 -> T=0.337

   -2<v_x<2  -2<v_y<2  인 경우 -> T=1.351

    * 모든 그래프는 히스토그램을 나타내고 W()는 빈도를 뜻한다.

   1. 위치적으로 입자가 공간에 고루 퍼져 있는 상태가 가장 높은 경우의 수이다.

  어느 한 곳이 입자가 없어져서 진공이 되는 경우는 없다.

   2. 가장 높은 경우의 수인 Maxwell velocity distribution 만족

   ε=p²/2m 일 때 ( 분자간 상호작용 무시 , 이상기체 )

   g(v_x) dv_x ∝ e^{-v_x^2/2T} dv_x

    * g(v_x) 는 단위 부피당 v_x 와 v_x + dv_x 사이에 있는 평균 입자 갯수

   초기에는  -1<v_x<1  -1<v_y<1   -2<v_x<2  -2<v_y<2  에서 uniform 분포를 보였지만 평형에 도달한 후

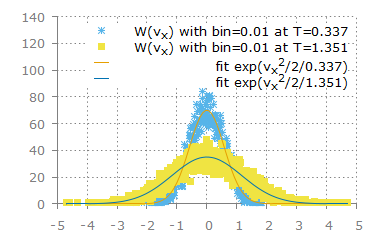
    즉 충돌을 통해서 에너지를 교환하는 경우에 가장 높은 경우의 수에 해당하는 맥스웰-볼츠만 속력 분포를 보임을 알 수 있다.

    높은 온도의 입자들은 좀 더 퍼져 있는 경향을 보이고 낮은 온도의 입자들은 분포가 0 근처에서 더 뾰족하다.

    ( v_y 의 모습도 마찬가지이다. ) 

    위 그래프에 로그를 취한 후 v_x² 를 x축으로 하였을 때 기울기가 1/2T 에 해당하므로

    ln(g(v_x)) ∝ -v_x²/2T

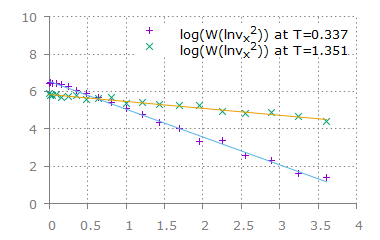
   기울기 :  -1.486   그래프를 통해 얻은 온도 T = 1/1.486/2=0.336

   기울기 :  -0.369   그래프를 통해 얻은 온도 T = 1/0.369/2=1.355

   고정된 에너지 값을 가지고 등분배 정리를 통해 얻은 값과 거의 일치함을 알 수 있다.  

   속력에 대한 분포는 2차원이므로

   F(v)dv ∝ ∫ f(v) d²v

   F(v)dv ∝ v*exp(-v²/2T)

    * F(v)dv 는 단위 부피당 v와 v+dv 사이에 있는 평균 입자 갯수

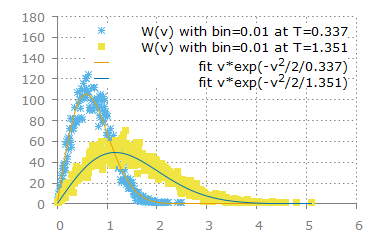
   속력에 대한 분포는 2차원에서는 같은 속력인 경우의 수가 속력이 커질수록 증가하므로 앞에 v가 곱해졌고

   그로 인하여 peak 지점이 0이 아닌 지점이고 오른쪽으로 옮겨간 모습이다.

   3. 위에서 얻은 그래프는 속력에 대한 그래프이다. 각 입자가 가지고 있는 에너지를 가지고 그래프를 그려보면

     평형일 때 볼츠만 분포를 만족한다. 한편 입자가 충돌하면서 얻거나 잃은 |ΔE| (에너지 변화의 절대값)를 추적하여

     빈도를 그래프로 그려보았을 때 아래와 그림과 같았다.

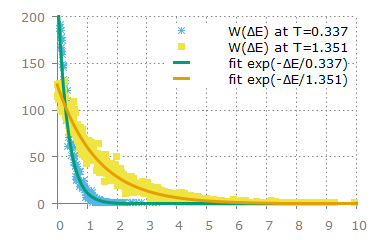
    에너지의 변화의 절대값 역시 각각의 온도에 해당하는 볼츠만 분포를 따랐다.

   4. 에너지가 작은 입자 (속력이 작은 입자) 와 에너지가 큰 입자 (속력이 큰 입자) 의 첫번째 충돌을 추적하였다.

     3번의 그래프는 에너지 변화의 절대값 그래프이다. 충돌할때 한 입자는 에너지를 잃고 한 입자는 에너지를 얻는데 이 값이 같으므로

     전체 입자의 에너지 변화의 히스토그램은 좌우 대칭이고 평균값이 0이다. 한편 어느 한 에너지 값의 입자의 에너지 변화만 살펴보자.

     T=1.351 일 때 에너지가 0.9 - 1.1 에 해당하는 입자들과  에너지가 2.8 - 3.2 에 해당하는 입자들을 뽑아서 충돌을 관찰하였고  

     에너지가 0.9 - 1.1 에 해당하는 입자들은 평균 에너지보다 작은 입자들이고 에너지가 2.8 - 3.2 에 해당하는 입자들은 평균 에너지보다 큰 입자다.

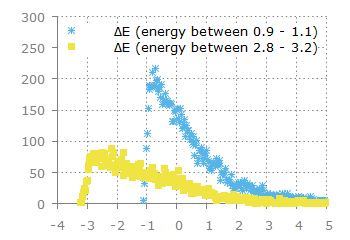
    에너지가 큰 입자는 충돌을 통해서 에너지를 잃을 경향성이 크다.     ( 평균 ΔE : -1.02 < 0  )

    에너지가 작은 입자는 충돌을 통해서 에너지를 얻을 경향성이 크다.  ( 평균 ΔE : 0.48 > 0  )

결론

    통계역학에서 경우의 수로 기술되는 볼츠만 분포가 충돌을 통해서 에너지를 교환하는 자연계(이상기체로 근사)를 잘 설명한다.

사용된 C언어 소스

   c파일 : 초기 조건 부여 후 평형 상태까지 시뮬레이션

   c파일 : 평형 상태의 값들을 이용해서 ΔE계산

   c파일 : 평형 상태의 값들을 이용해서 높은 에너지의 와 낮은 에너지의 ΔE 계산

참고 문헌  

    Fundamentals of Statistical and Thermal Physics / F. Reif